In English, we often drop the subject of a phrase:

Who are these signs written for? It's reallyYou, stoporYou, yieldorYou, be alert for bears(I'm not doing it).
在内化一门语言之后,我们可以在没有明确指示的情况下获得暗示。但是,礼貌地说,数学通常不是很内化。
让我们弄清楚“数学符号”指的是谁。
Imaginary Numbers
Imaginary numbers are often defined as $i^2 = -1$, and written this way they're utterly baffling.
A better restatement is:
![]()
这还是让人困惑。But what about this:
![]()
It's getting clearer. The instructions are: "Start with 1, multiply by i, multiply by i again, and (somehow) end up at -1".
What could do that? Realizing westart at 1 and end up at -1helps us visualize something like this:
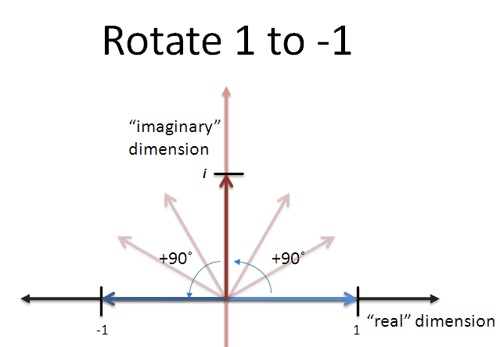
Aha! $i$ is a change (visualized as a rotation) that moves us from positive to negative in two steps (More about imaginary numbers.)
Writing $i^2 = -1$ without a clear subject is confusing. (Don't get me started with $i = \sqrt{-1}$)
Missing the implied subject of "1" in $1* i * i$ caused me years of confusion. I wish this sign was hanging on the classroom wall:

Exponents
为什么x^0对任何x值都是1 ?我们如何要求0的东西,然后得到1 ?
Again, let's break it down with a simple example. Here's a typical exponent:
![]()
但缺了一个主题。It's written better as:
![]()
We start at 1 (our default multiplicative scaling factor), scale by x, then scale by x again, ending up at $x^2$. The size of the exponent (2) tells us the number of times to use our "times x" scaling machine.
Stepping back, multiplication is about scaling: 3 is really "1 * 3", or the unit quantity enlarged 3 times.
If we want to scale by x (just once), we write:
![]()
What if we don't plan on using our scaling machine at all?
![]()
这个符号有点奇怪,但我用了空括号表示没有动作。你看,x^0$中的零代表漠不关心,不采取行动,而不是毁灭。使用x^0表示我们根本没有扩大原始量。
微妙的,对吧?
We can take this "growth machine" idea further with theExpand-o-tron 3000.
Imaginary Exponents
Let's combine insights. What does a strange exponent like $e^{i \pi}$ represent?
With our new "implicitly start at 1" perspective, it's really:
![]()
Start at 1 and then apply the growth engine. Here, growth is aimed sideways ($i$) with enough fuel to last for half a circle ($\pi$).
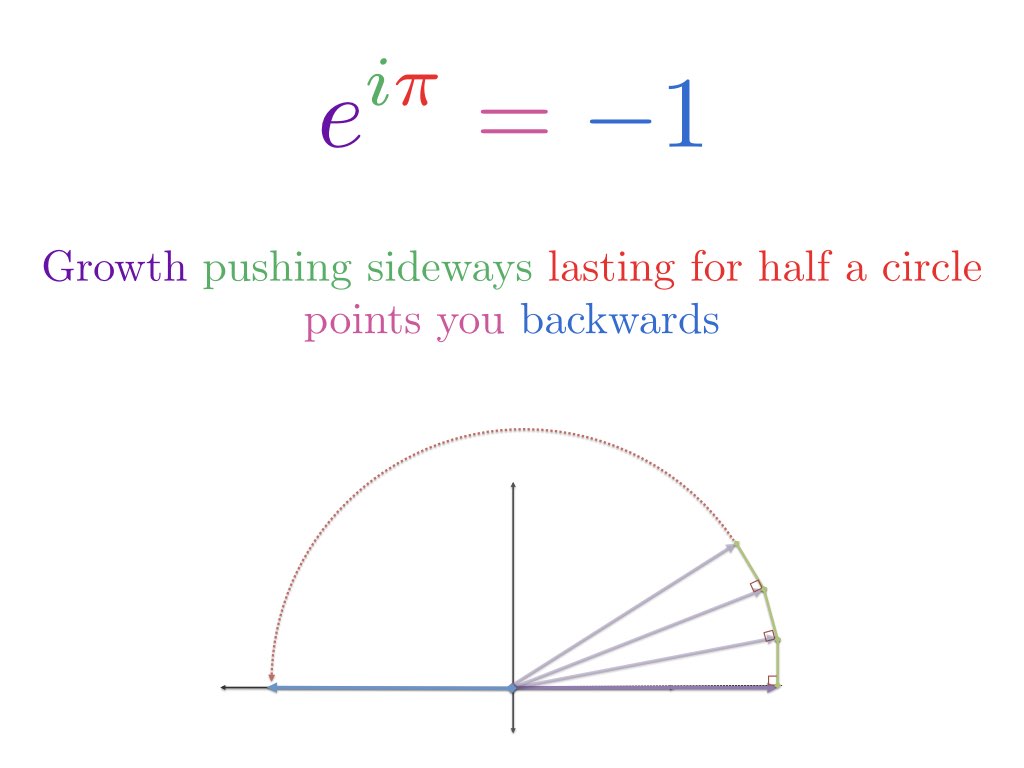
The essence of Euler's Identity is that we are starting at 1 and transforming it with a spin. We aren't creating a negative number out of seemingly positive exponents directly. (See article and video.)
Calculus
微积分有许多快捷符号。When we write:
![]()
it really means:
![]()
which really means:
![]()
Here's the tricky part. There isn't a single "dx", there's a whole chain of them along the number line. The sentence is something like:
"Hey everyone on the number line! You're all spaced "dx" apart. Take your current position and square it. Then I'll come by and add you all up."
The integral addresses not a single "you" like 1.0, but "them", the countless positions on the number line.
Find the implied subject in an equation, then work to shorten it (Bears!).
快乐数学。