指数是什么意思?

Ever get a hint of confusion about what an exponent was doing? I sure have.

Like the word "run", the meaning depends on context:

• crawl / walk / run (movement)
• run a company (general operation)
• a run of good luck (sequence)
• and adozen more definitions

Sticking with a single interpretation of "run" leads to confusion, and the same happens in math. Let's clarify how exponents are used.

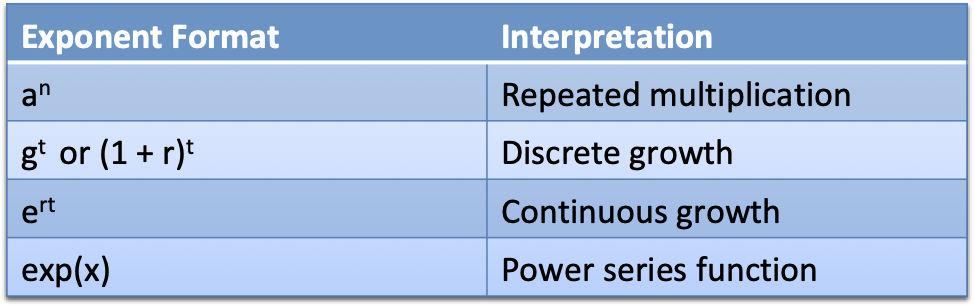
Meaning 1: Repeated Multiplication

We first learn that exponents like $3^2$ or $a^n$ are repeated multiplication: multiply $a$, $n$ times.

就像用手指数一样，这可以分解到正整数之外。分数指数是什么意思?消极的?零?(因为$a^0 = 1$，我们用0乘以得到1?)

Common usage of $a^n$:Counting problems. If you flip a coin $n$ times, you have $2^n$ possible outcomes.

Meaning 2: Growth Microwave

Let's say I have an exponent like $3^{4.5}$. I mentally convert it to $1.0 * 3^{4.5}$, and then $1.0 * g^{t}$.

With the"growth microwave"analogy, an exponent grows our starting amount (1.0) by $g$ for $t$ units of time. (In this example, 3x growth applied for for 4.5 seconds.)

What values can $t$ have?

• If t is positive, we go forward in time and get larger (assuming $g > 1$). Fractional time is ok -- I can run a microwave for 3.5 minutes, and get some effect between 3 minutes and 4 minutes.
• If t is negative, we go backwards in time and get smaller. If a regular microwave allowed negative time, it would cool down your food, right?
• If t is zero, we didn't use the machine at all! We're left with 1.0, our original amount.

The growth microwave interpretation helps with fractional powers (and resolves the t=0 issue), but it's notflexible. Doubling the rate and halving the time doesn't have the result we expect:

2 seconds of 3x growth isn't the same as 1 second of 6x growth. Ugh. I'm not a caveman, we need to mix rate and time! (Hold onto that thought.)

Common usage of $g^t$: Man-made systems. If I agree to pay you 15% at a certain discrete interval (yearly), we can model the outcome as $(1.15)^t$. If I decide to cut the payments short (2.5 years) we can exponentially interpolate between the two intervals ($r^{0.5}$ is the square root). We often set $g = (1 + r)$, so we could write $(1 + .15)^t$.

旁白:让我们证明$g^t$是不灵活的。

However, this shows the special case of $2^2 = 4^1$ does work.

Meaning 3: Continuous Growth Engine

Regular readers know I think of e as a continuous growth engine:

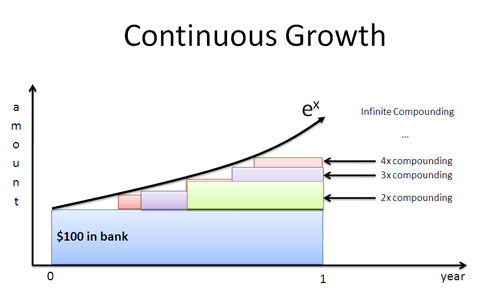
Instead of waiting to grow at discrete intervals, we apply interest immediately and compound as fast as we can. A pleasant consequence ofe's definitionis that we merge rate and time into a single, interchangeable quantity:

Conveniently, 2 years of 50% growth is the same as 1 year of 100% growth. We doubled our rate, halved our time, and got the same result. (Practically, we may prefer the shorter time period but the final quantity is the same.)

输入$x$是“生长燃料”，可以分离为“速率*时间”。基数e是一个只关心你给它多少燃料的机器。在50个时间段内滴入燃料，或者用消防水管将其注入一个时间段内。无论哪种方式，相同的总输入$x$得到相同的最终结果。

Common usage of $e^{rt}$:自然系统。大多数物理定律都有持续增长的模式(赚取利息和使用利息之间没有延迟)。为了方便起见，我们有时可以用人造的说法，例如，即使原子在瞬间衰变，我们也可以用20年的放射性半衰期来描述。

(Aside: Use the2022世界杯预选赛 to convert one exponent format to another. $g^t = e^{\ln(g)t}$)

Meaning 4: A Power Series Calculation

We can treat $e^x$ as a fancy mathematical function:

You may see $e^x$ written $\exp(x)$, treated like any other function $f(x)$. Here, $x$ is just a numerical input to an intricate power series. Concepts like repeated counting, growth rate, and time fall into the background (though we cansee them if we look).

Curiously, we're left with integer powers ($x^0, x^1, x^2, x^3$) and our "repeated multiplication" interpretation shows up again! The power of the exponent, $x$, switches from the number of multiplications to the base being multiplied. (Theciiiircleof life.)

Common usage of $\exp(x)$: When we see $e^x$ as just another function, a few properties emerge:

• Usingcalculus with exponentsgets way easier, since we can take the derivative / integral of each term (and realize $\frac{d}{dx} e^x = e^x$).
• Exponential approximations become easy: $e^x \sim 1 + x$ for small values of $x$, since the higher-order powers become negligible.
• Other math patterns click. Sine and cosine have expansions similar to $e^x$, hinting that trig functions and exponents are connected (Euler's Formula).
• $e^x$ looks like a polynomial of infinite degree, and will eventually surpass any finite polynomial. (While $x^2 + 100 > e^x$ in the beginning, $e^x$ will eventually exceed it.)

So which version of exponents is best?

You probably guessed it: it depends, though the interpretations are listed from most to least common for a general audience.

If a formula doesn't make sense, try switching versions. Life's too short to have only a single interpretation of exponents.

Happy math.

Other Posts In This Series

1. An Intuitive Guide To Exponential Functions & e
2. 2022世界杯预选赛
3. A Visual Guide to Simple, Compound and Continuous Interest Rates
4. Common Definitions of e (Colorized)
5. 理解指数(为什么0^0 = 1?)
6. Using Logarithms in the Real World
7. How To Think With Exponents And Logarithms
8. Understanding Discrete vs. Continuous Growth
9. 指数是什么意思?
10. Q: Why is e special? (2.718..., not 2, 3.7 or another number?)